Ch4.2 拓扑群和轨道空间
4.3 拓扑群
考虑一些除了拓扑结构外还具有群结构的空间。一个典型例子是圆周,可将其视作模为1的复数集合。其拓扑由平面诱导,群结构则由复数乘法构成。注意以下两个映射
$$ S^1 \times S^1 \to S^1, \quad (e^{i\theta}, e^{i\phi}) \mapsto e^{i(\theta + \phi)} \quad \text{(群乘法)} $$
$$ S^1 \to S^1, \quad e^{i\theta} \mapsto e^{-i\theta} \quad \text{(取逆元)} $$
都是连续的,因此拓扑结构与代数结构完全相容。
定义 4.14
拓扑群 $G$ 是一个豪斯多夫拓扑空间,同时也是一个群,且两种结构相容,即群乘法 $m: G \times G \to G$ 以及将每个元素映射为其逆元的映射 $i: G \to G$ 均连续。
本节内容主要通过例子展开,包括矩阵群的例子。在第4.4节,我们将回到商空间,定义拓扑群在空间上的作用,展示此类作用如何产生商空间,并考察由此得到的各种商空间。
拓扑群的例子
- 实直线:群结构为实数加法。
- 圆周:如上所述。
- 离散群:任何抽象群赋予离散拓扑。
- 环面:视为两个圆周的乘积,采用乘积拓扑与乘积群结构。(两个拓扑群的乘积仍为拓扑群。)
- 三维球面:视为四元数空间 $\mathbb{H}$(拓扑同胚于 $\mathbb{E}^4$ 并具有四元数代数结构)中的单位球。
- 欧几里得 $n$ 维空间:记作 $\mathbb{R}^n$ 以强调其作为拓扑群(通常以加法为群结构),而非单纯的拓扑空间 $\mathbb{E}^n$。
- 一般线性群 $\mathrm{GL}(n)$:由实数域上 $n \times n$ 可逆矩阵构成,群结构为矩阵乘法。将矩阵 $A = (a_{ij})$ 与点 $(a_{11}, \dots, a_{nn}) \in \mathbb{E}^{n^2}$ 等同,赋予子空间拓扑。定理(4.12)将验证 $\mathrm{GL}(n)$ 是一个拓扑群。
- 正交群 $\mathrm{O}(n)$:由 $n \times n$ 正交实矩阵构成,其拓扑与代数结构均从 $\mathrm{GL}(n)$ 诱导而来,是 $\mathrm{GL}(n)$ 的子群。其中行列式为 $+1$ 的矩阵构成特殊正交群 $\mathrm{SO}(n)$。
对于拓扑群,“同构”与“子群”需同时考虑拓扑与代数结构。因此,拓扑群之间的同构既是同胚也是群同构;子群需在代数上是子群,并具有子空间拓扑。
例:整数集 $\mathbb{Z}$ 赋予离散拓扑构成 $\mathbb{R}$ 的子群。商群 $\mathbb{R}/\mathbb{Z}$ 赋予商拓扑(划分由 $\mathbb{Z}$ 的陪集给出)同构于圆周 $S^1$。映射 $f: \mathbb{R} \to S^1, f(x)=e^{2\pi i x}$ 是商映射,诱导同胚 $\mathbb{R}/\mathbb{Z} \cong S^1$,该同胚也是群同构。
例:将每个 $(n-1)\times(n-1)$ 正交矩阵 $A$ 对应到 $n\times n$ 矩阵 $\begin{pmatrix}1 & 0 \\ 0 & A\end{pmatrix}$,表明 $\mathrm{O}(n-1)$ 同构于 $\mathrm{O}(n)$ 的一个子群。
设 $G$ 为拓扑群,$x \in G$。映射 $L_x(g)=xg$(左平移)与 $R_x(g)=gx$(右平移)均为同胚。这表明拓扑群具有“齐性”:任意两点 $x,y \in G$,存在同胚 $L_{yx^{-1}}$ 将 $x$ 映至 $y$,故 $G$ 在各点附近局部拓扑相同。
定理 4.15
设 $G$ 为拓扑群,$K$ 为包含单位元 $e$ 的连通分支。则 $K$ 是 $G$ 的闭正规子群。对于 $G = \mathrm{O}(n)$,有 $K = \mathrm{SO}(n)$(证明稍后给出)。
证明:连通分支总是闭的。对任意 $x \in K$,集合 $Kx^{-1}=R_{x^{-1}}(K)$ 连通且包含 $e$,故 $Kx^{-1} \subseteq K$,从而 $KK^{-1}=K$,即 $K$ 为子群。对任意 $g \in G$,$gKg^{-1}=R_{g^{-1}}L_g(K)$ 连通且包含 $e$,故 $gKg^{-1} \subseteq K$,即 $K$ 正规。
定理 4.16:单位元的邻域是生成元
在连通拓扑群中,单位元的任意邻域都能生成整个群。
证明:设 $G$ 连通,$V$ 是 $e$ 的邻域,令 $H=\langle V \rangle$。对任意 $h \in H$,邻域 $hV=L_h(V) \subseteq H$,故 $H$ 开。下证 $G-H$ 亦开:若 $g \in G-H$,则邻域 $gV$ 若与 $H$ 相交将导致 $g \in H$,矛盾,故 $gV \subseteq G-H$。由于 $G$ 连通且 $H$ 非空,必有 $G-H=\varnothing$,即 $G=H$。
定理 4.17
矩阵群 $\mathrm{GL}(n)$ 是拓扑群。
证明:记 $\mathbb{M}$ 为所有 $n\times n$ 实矩阵集合,通过对应 $(a_{ij}) \leftrightarrow (a_{11},\dots,a_{nn}) \in \mathbb{E}^{n^2}$ 赋予拓扑。矩阵乘法 $m: \mathbb{M} \times \mathbb{M} \to \mathbb{M}$ 连续,因为其各分量 $\pi_{ij} \circ m(A,B)=\sum_k a_{ik}b_{kj}$ 是多项式,故连续。$\mathrm{GL}(n)$ 取子空间拓扑,则乘法 $\mathrm{GL}(n) \times \mathrm{GL}(n) \to \mathrm{GL}(n)$ 连续。
验证逆映射 $i: \mathrm{GL}(n) \to \mathrm{GL}(n)$ 连续:$i$ 的分量映射将 $A$ 映至 $A^{-1}$ 的 $(j,k)$ 元,即 $(1/\det A)$ 乘以 $A$ 的相应余子式。由于 $\det A$ 及余子式均为 $A$ 的元素的多元多项式,且 $\det A \ne 0$,故各分量连续,从而 $i$ 连续。
$\mathrm{GL}(n)$ 是行列式函数 $\det: \mathbb{M} \to \mathbb{R}$ 下非零实数的原像,故为 $\mathbb{M}$ 的开子集,非紧。其可划分为行列式正、负两个连通分支。
定理 4.18
$\mathrm{O}(n)$ 与 $\mathrm{SO}(n)$ 是紧致的。
证明:$\mathrm{O}(n)$ 由满足 $AA^t = I$ 的矩阵构成。定义映射 $f_{ik}: \mathbb{M} \to \mathbb{E}^1$,$f_{ik}(A)=\sum_j a_{ij}a_{kj}$。则 $\mathrm{O}(n)$ 是所有 $f_{ik}^{-1}(0) (i\ne k)$ 与 $f_{ii}^{-1}(1)$ 的交集,故为 $\mathbb{M}$ 中闭集。由条件 $\sum_j a_{ij}^2=1$ 知矩阵各元绝对值 $\le 1$,故 $\mathrm{O}(n)$ 有界,从而是 $\mathbb{E}^{n^2}$ 的紧子集。$\mathrm{SO}(n)$ 作为 $\mathrm{O}(n)$ 的闭子集亦紧。
注记
$\mathrm{SO}(2) \cong S^1$(对应 $e^{i\theta} \leftrightarrow \begin{pmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{pmatrix}$);$\mathrm{SO}(3) \cong P^3$(通过将单位四元数 $S^3$ 共轭作用视为三维旋转,诱导商映射 $S^3 \to \mathrm{SO}(3)$,其核为 $\{\pm1\}$,故得同构 $P^3 = S^3/\{\pm1\} \cong \mathrm{SO}(3)$)。
4.4 轨道空间
无限循环群 $\mathbb{Z}$ 可自然地视作实直线上的一个同胚变换群,其中每个整数 $n \in \mathbb{Z}$ 确定一个平移变换 $x \mapsto x + n$。
考虑正交矩阵群 $O(n)$,每个矩阵诱导出欧几里得 $n$ 维空间的一个线性变换。由于 $O(n)$ 的元素可逆且保持欧几里得度量(因而将单位向量映为单位向量),每个正交矩阵给出了单位球面 $S^{n-1}$ 到自身的同胚。正交群在球面上的作用与 $O(n)$ 及 $S^{n-1}$ 的拓扑相容,因为映射
$$ O(n) \times S^{n-1} \to S^{n-1}, \quad (A, x) \mapsto Ax $$
连续。我们称 $O(n)$ “作用”于空间 $S^{n-1}$。
若赋予 $\mathbb{Z}$ 由 $\mathbb{R}$ 诱导的自然离散拓扑,则上述两例均符合以下一般框架。
定义 4.14
设 $G$ 为拓扑群,$X$ 为拓扑空间。若满足以下条件,则称 $G$ 作为同胚变换群作用于 $X$:
- 对所有 $g,h \in G$ 及 $x \in X$,有 $hg(x) = h(g(x))$;
- 对所有 $x \in X$,有 $e(x) = x$,其中 $e$ 是 $G$ 的单位元;
- 映射 $G \times X \to X$,$(g,x) \mapsto g(x)$,连续。
对任意 $x \in X$,每个 $g \in G$ 对应的同胚或固定 $x$,或将其映至新点 $g(x)$。当 $g$ 取遍 $G$ 时,所有像 $g(x)$ 构成的子集称为 $x$ 的轨道,记作 $O(x)$。若两轨道相交,则它们必重合。关系 $x \sim y \iff \exists g \in G,\ x = g(y)$ 是 $X$ 上的等价关系,其等价类恰为轨道。因此轨道构成 $X$ 的一个划分,相应的商空间称为轨道空间,记作 $X/G$。构造 $X/G$ 即通过 $G$ “除” $X$:两点被视为相同当且仅当它们相差某个同胚 $x \mapsto g(x)$。
在第一例中,实数 $x$ 的轨道包含所有形如 $x + n$($n \in \mathbb{Z}$)的点。故在构成 $\mathbb{R}/\mathbb{Z}$ 时,我们将 $\mathbb{R}$ 中相差整数的点等同,如前节所述,得到轨道空间为圆周。
球面上的正交作用是传递作用之例,即任意点的轨道均为整个空间(此处为 $S^{n-1}$)。证明简述如下:设 $e_1, e_2, \dots, e_n$ 为 $\mathbb{E}^n$ 的标准正交基,对任意 $x \in S^{n-1}$,构造以 $x$ 为首个基向量的新正交基。记该新基相对于 $e_1, e_2, \dots, e_n$ 的过渡矩阵为 $A$,则 $A$ 正交且 $A(e_1) = x$。这即表明 $e_1$ 的轨道为整个 $S^{n-1}$。当作用传递(仅有一个轨道)时,轨道空间显然为单点。
更多示例
-
环面:将第一例与其自身作积,自然地得到 $\mathbb{Z} \times \mathbb{Z}$ 在平面上的作用:$(m,n) \in \mathbb{Z} \times \mathbb{Z}$ 将 $(x,y) \in \mathbb{E}^2$ 映至 $(x+m, y+n)$。轨道空间是两个圆周的积,即环面。几何上,此作用保持由过整数坐标点的水平与垂直线划分的单位正方形网格。每个正方形包含每个轨道的一点,在商映射 $\pi: \mathbb{E}^2 \to \mathbb{E}^2 / (\mathbb{Z} \times \mathbb{Z}) = T$ 下,正方形的边按通常方式等同,得到环面 $T$。
-
射影空间:定义 $\mathbb{Z}_2$ 在 $n$ 维球面 $S^n$ 上的作用,使其轨道空间为射影空间 $P^n$。$\mathbb{Z}_2$ 仅含两个元素:单位元对应恒等同胚,生成元对应对径映射 $x \mapsto -x$(注意此同胚的平方为恒等)。轨道为对径点对,轨道空间即对应第 4.2 节中 $P^n$ 的一种描述。
-
环面上的三种 $\mathbb{Z}_2$ 作用:考虑 $\mathbb{E}^3$ 中由圆 $(x - 3)^2 + z^2 = 1$ 绕 $z$ 轴旋转生成的环面 $T$。令 $g$ 为 $\mathbb{Z}_2$ 的生成元,定义:
- $g(x,y,z) = (x, -y, -z)$(绕 $x$ 轴旋转 $\pi$);
- $g(x,y,z) = (-x, -y, z)$(绕 $z$ 轴旋转 $\pi$);
- $g(x,y,z) = (-x, -y, -z)$(关于原点的反射)。
每个同胚确定 $\mathbb{Z}_2$ 在 $T$ 上的一个作用,其轨道空间分别为球面、环面与克莱因瓶(见图 4.3)。每种情形下,$g$ 交换两柱面 $C_1$ 与 $C_2$,故为构造轨道空间可忽略 $C_2$,仅需在 $C_1$ 的边界圆上进行适当等同。
-
子群的左作用与右作用:设 $G$ 为拓扑群,$H \leq G$。$H$ 通过左平移 $L_h(g) = hg$ 作用于 $G$,映射 $H \times G \to G$ 连续(因乘法连续)。两元素 $g, g'$ 属于同一轨道当且仅当 $g' \in Hg$,故轨道为 $H$ 在 $G$ 中的右陪集。类似地,$H$ 也有右作用 $(h,g) \mapsto R_{h^{-1}}(g) = gh^{-1}$,此时轨道为左陪集。这两种轨道空间同胚,均记作 $G/H$。
-
正交群的齐性空间:回到 $O(n)$ 在 $S^{n-1}$ 上的作用。若 $A \in O(n)$ 满足 $A(e_1) = e_1$,则 $A$ 形如
$$ \begin{pmatrix} 1 & 0 \\ 0 & B \end{pmatrix}, $$
其中 $B$ 正交;反之亦然。故固定 $e_1$ 的子群同构于 $O(n-1)$。定义连续满射 $f: O(n) \to S^{n-1}$,$f(A)=A(e_1)$。由于 $O(n)$ 紧致且 $S^{n-1}$ 豪斯多夫,$f$ 为商映射(推论 4.4)。对 $x \in S^{n-1}$,取 $A \in O(n)$ 使 $A(e_1)=x$,则 $f^{-1}(x)$ 恰为左陪集 $AO(n-1)$。故 $f$ 诱导的划分与子群 $O(n-1)$ 的左陪集分解一致,由定理 4.2 知 $O(n)/O(n-1) \cong S^{n-1}$。类似有 $SO(n)/SO(n-1) \cong S^{n-1}$。
由此可归纳证明 $SO(n)$ 连通:$SO(1)$ 为单点;对 $n \geq 1$,$S^n$ 连通,且由以下定理保证归纳步骤。定理 4.15 设 $G$ 作用于 $X$。若 $G$ 与 $X/G$ 均连通,则 $X$ 连通。
证明概要:若 $X$ 可分解为两非空不相交开子集 $U, V$ 之并,则由于商映射 $\pi$ 将开集映为开集且 $X/G$ 连通,$\pi(U)$ 与 $\pi(V)$ 必相交。取 $\pi(x) \in \pi(U) \cap \pi(V)$,则 $U \cap O(x)$ 与 $V \cap O(x)$ 非空且构成轨道 $O(x)$ 的一个分割。但 $O(x)$ 作为连续映射 $g \mapsto g(x)$ 的像连通,矛盾。 -
透镜空间:设 $p, q$ 为互素整数。视三维球面为复二维空间中的单位球面:
$$ S^3 = \{(z_0, z_1) \in \mathbb{C}^2 \mid |z_0|^2 + |z_1|^2 = 1\}. $$
令 $g$ 为循环群 $\mathbb{Z}_p$ 的生成元,定义 $\mathbb{Z}_p$ 在 $S^3$ 上的作用为
$$ g(z_0, z_1) = (e^{2\pi i / p} z_0, e^{2\pi i q / p} z_1). $$
$g$ 作用 $p$ 次后回到恒等。商空间 $S^3/\mathbb{Z}_p$ 称为透镜空间,记作 $L(p,q)$。它是局部欧几里得的三维流形,其基本群同构于 $\mathbb{Z}_p$。 -
环面上的无理流:此例给出实直线在环面上的一个作用,其中每条轨道是环面的一个稠密真子集。将环面等同于 $S^1 \times S^1$,定义 $r \in \mathbb{R}$ 诱导的同胚为
$$ (e^{2\pi i x}, e^{2\pi i y}) \mapsto (e^{2\pi i (x + r)}, e^{2\pi i (y + r\sqrt{2})}). $$
令 $\pi: \mathbb{E}^2 \to S^1 \times S^1$ 为商映射 $(x,y) \mapsto (e^{2\pi i x}, e^{2\pi i y})$,则作用的轨道即 $\pi$ 下平面中斜率为 $\sqrt{2}$ 的直线的像。由于 $\sqrt{2}$ 无理,$\pi$ 限制在此类直线上为单射。考察点 $\pi(0,0)$ 的轨道:它是过原点(或任意整点)斜率为 $\sqrt{2}$ 的直线在 $\pi$ 下的像。该轨道在环面上反复缠绕,构成一个稠密集但非整个环面。此作用称为环面上的无理流,轨道称为流线。 -
平面晶体学群:考虑保持平面某种凸多边形铺砌图案的等距变换群。图 4.5 给出三例生成元示意:平移用箭头 $\longrightarrow$ 表示;滑动反射(沿直线的反射复合沿该直线的平移)用半箭头 $\longrightarrow$ 表示;绕线段中点的 $180^\circ$ 旋转(半转)用 $\curvearrowright$ 表示。每图中阴影区域为该群的基本区域,即其在所有群元素下的像铺满平面,且任意两像之交仅含边界点。基本区域不唯一。
- 生成元:两个平移;轨道空间:环面。
- 生成元:三个半转;轨道空间:球面。
- 生成元:两个平行滑动反射;轨道空间:克莱因瓶。
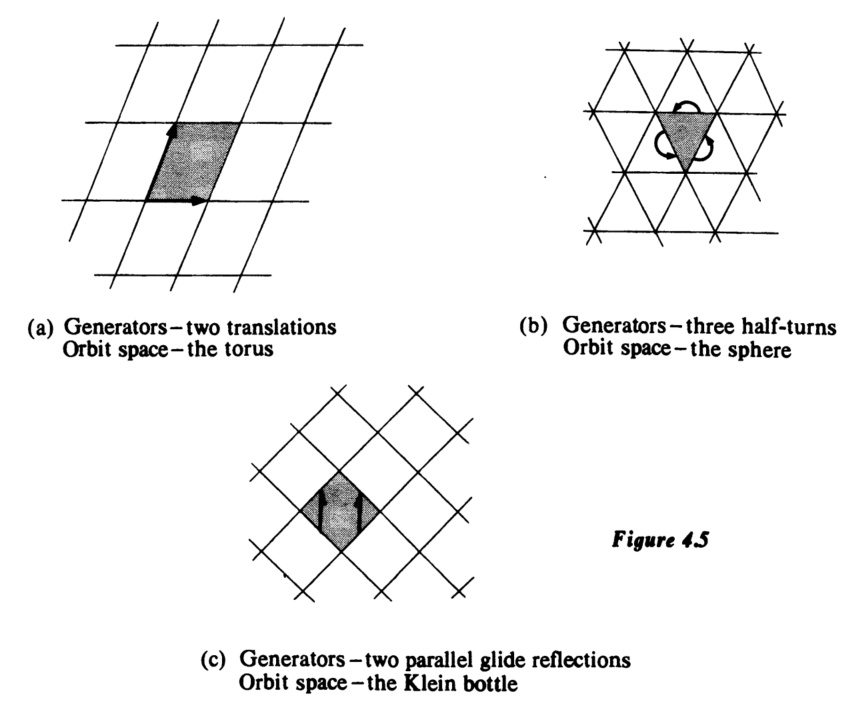
这些群可置于以下统一框架:平面等距变换群可表为有序对 $(\theta, \mathbf{v})$,其中 $\theta \in O(2)$,$\mathbf{v} \in \mathbb{E}^2$。作用为 $(\theta, \mathbf{v})(\mathbf{x}) = \theta(\mathbf{x}) + \mathbf{v}$,群乘法为 $(\theta, \mathbf{v})(\phi, \mathbf{w}) = (\theta\phi, \theta(\mathbf{w}) + \mathbf{v})$。赋予其 $O(2) \times \mathbb{E}^2$ 的乘积拓扑,所得拓扑群称为欧几里得群 $E(2)$(代数结构为 $O(2)$ 与 $\mathbb{E}^2$ 的半直积)。
若 $G$ 是 $E(2)$ 的离散子群(诱导拓扑使 $G$ 离散),且轨道空间 $\mathbb{E}^2/G$ 紧致,则称 $G$ 为平面晶体学群。上述三例均为平面晶体学群。对这样的 $G$,若取 $p \in \mathbb{E}^2$ 不被任何非单位元固定,则集合
$$ \{x \in \mathbb{E}^2 \mid \|x - p\| \leqslant \|x - g(p)\|,\ \forall g \in G\} $$
是一个凸多边形基本区域,且 $G$ 是平面对称群的一个有限指数子群。$\mathbb{E}^2/G$ 的紧致性保证该区域有界。平面晶体学群可完全分类,共 17 个不同同构类。高维晶体学群可类似定义,对固定维数,其同构类数目有限。