基于稳定子表的量子电路模拟

第2部分：模拟算法

2.1：泡利框架模拟

断言（坍缩操作）

一个坍缩操作¹⁴ 可能会引入一个新的稳定子 $S$。以下两种模拟随机测量的方法是等价的：

• 忠实地报告结果。（不对泡利框架 $\mathcal{F}$ 做任何操作。）
• 总是报告 $+1$。以 50% 的概率将 $S$ 应用于泡利框架 $\mathcal{F}$。

¹⁴ 初始化、重置、测量。

例（忠实地模拟 vs 泡利框架模拟）

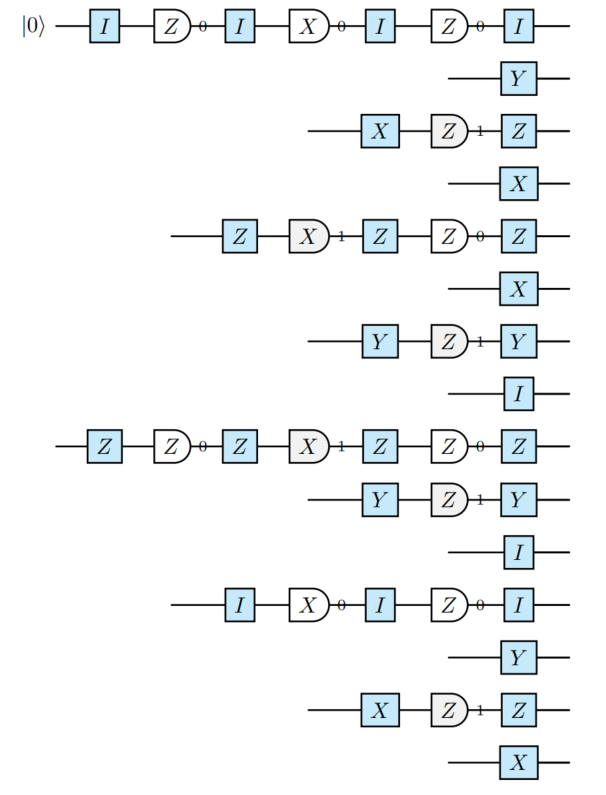
以下两个电路是等价地模拟一个单量子比特电路（包含一次初始化和三次（随机）测量）的方法。¹⁵

¹⁵ 泡利框架在电路中通过蓝色块指示。

---

忠实地模拟

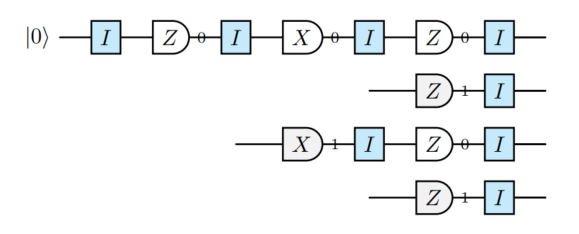
泡利框架模拟

---

断言（测量二分法）

设 $|\psi\rangle$ 是一个稳定子态，$M$ 是一个泡利可观测量。测量结果 $m \in \{+1, -1\}$ 是一个随机变量，具有以下两种可能分布之一：

• 确定性：如果 $P$ 与 $\mathcal{S}(|\psi\rangle)$ 中的所有生成元对易，则 $m$ 服从退化分布，即要么 $Pr[m=+1]=1$，要么 $Pr[m=-1]=1$。
• 均匀随机：如果 $P$ 与 $\mathcal{S}(|\psi\rangle)$ 中至少一个生成元反对易，则 $m \sim \mathcal{U}(\{+1, -1\})$，即 $Pr[m=+1] = Pr[m=-1] = 0.5$。

---

定义 14（参考样本）

设 $\mathcal{C}$ 是一个由克利福德门、泡利噪声信道、测量和重置组成的含噪稳定子电路。参考样本 $R$ 是通过模拟理想电路 $\mathcal{C}_{\text{ref}}$ 得到的测量结果记录，其中：

1. 所有泡利噪声信道在 $\mathcal{C}$ 中被替换为恒等操作。
2. 所有坍缩操作被偏置为确定性地产生 $+1$。

---

定义 15（概率赋值）

符号 $x \leftarrow_p y$ 表示变量 $x$ 以概率 $p$ 被设为 $y$，并以概率 $1-p$ 保持不变。

---

算法（跟踪泡利框架）

为了使用泡利框架模拟一个含噪稳定子电路：

1. 参考样本：令 $R$ 为从理想化电路 $\mathcal{C}_{\text{ref}}$¹⁶ 得到的参考测量记录。
2. 初始化：设置 $\mathcal{F} \leftarrow I^{\otimes n}$。对于每个初始化为 $|0\rangle$ 的量子比特 $q$：
   $$ \mathcal{F} \leftarrow_{0.5} \mathcal{F} Z_q $$
3. 执行：对电路中的每个操作 $O_i$：
   • 克利福德门 $C$：通过共轭更新框架：
     $$ \mathcal{F} \leftarrow C \mathcal{F} C^\dagger $$
   • 重置 $q$：
     (a) 设置 $\mathcal{F}_q \leftarrow I$。
     (b) 随机化框架 $\mathcal{F} \leftarrow_{0.5} \mathcal{F} Z_q$。
   • 泡利噪声信道 $\mathcal{E}$：设该信道由 Kraus 算子 $E_k = \sqrt{p_k} P_k$ 给出，其中 $P_k$ 是泡利错误，出现概率为 $p_k$。从分布 $\{p_k\}$ 中采样索引 $k$，并更新框架：
     $$ \mathcal{F} \leftarrow \mathcal{F} P_k $$
   • 测量 $M_q$：令 $r \in R$ 为对应此测量的参考测量结果。
     (a) 计算框架翻转位 $b$：
     $$ b = \begin{cases} 1 & \text{若 } \{\mathcal{F}, M_q\} = 0 \\ 0 & \text{若 } [\mathcal{F}, M_q] = 0 \end{cases} $$
     (b) 报告结果 $m = r \oplus b$。
     © 随机化框架 $\mathcal{F} \leftarrow_{0.5} \mathcal{F} M_q$。

¹⁶ 例如，通过算法 2.2。

---

2.2：稳定子表模拟

备注（不变性）

概念上，$T$ 始终被维护为到目前为止已处理的克利福德前缀的累积逆的表。如果已处理的克利福德前缀是：
$$ U = C_t C_{t-1} \cdots C_1, $$
那么不变量是：
$$ T = \text{Tableau}(U^{-1}), $$
即，对于每个生成元 $g \in \{X_k, Z_k\}$，
$$ T(g) = U^{-1} g U. $$

---

断言（来自表的稳定子）

设 $C$ 是作用于 $n$ 个量子比特上的一个克利福德操作。状态 $C|0\rangle^{\otimes n}$ 的稳定子群由共轭后的 $Z$ 算子生成：
$$ \mathcal{S}(C|0\rangle^{\otimes n}) = \langle CZ_1C^{-1}, \dots, CZ_nC^{-1} \rangle \quad (2.1) $$

---

算法（跟踪稳定子表）

为了使用稳定子表模拟一个稳定子电路：

1. 初始化：将稳定子表 $T$ 初始化为单位表 $I$。
2. 执行：遍历电路操作 $O_1, O_2, \dots, O_m$：
   • 克利福德门 $C$：将门 $C$ 的逆表前置到当前表中：
     $$ T \leftarrow T \circ \text{Tableau}(C)^{-1} \quad (2.2) $$
   • 测量 $Z_q$：检查表 $T$ 中 $X_q$ 列，记作 $D_q$：
     • 情况 1：随机。如果存在 $p$ 使得 $\{(D_q)_p, Z_q\} = 0$（即 $(D_q)_p \in \{X,Y\}$）：
       (a) 选择一个主量子比特索引 $p$，使得 $(D_q)_p \in \{X,Y\}$。
       (b) 通过在电路开头插入一个 CNOT$_{p \to k}$ 来约化其他所有量子比特索引 $k \neq p$，其中 $(D_q)_k \in \{X,Y\}$。这会更新表：
       $$ T \leftarrow \text{Tableau}(\text{CNOT}_{p \to k}) \circ T \quad (2.3) $$
       © 通过在电路开头插入一个 $H_p$ 将泡利项 $(D_q)_p$ 转换为 $Z$。这会更新表：
       $$ T \leftarrow \text{Tableau}(H_p) \circ T \quad (2.4) $$
       (d) 通过在电路开头附加一个 $X_p$ 以 0.5 的概率随机化测量。这会更新表：
       $$ T \leftarrow_{0.5} \text{Tableau}(X_p) \circ T \quad (2.5) $$
       (e) 约化至确定性情况。
     • 情况 2：确定性。如果 $\forall k, [(D_q)_k, Z_q] = 0$（即 $(D_q)_k \in \{I,Z\}$），根据 $T$ 中 $Z_q$ 列的符号报告测量结果：
       $$ m = \begin{cases} 0 & \text{若符号为 } +1 \\ 1 & \text{若符号为 } -1 \end{cases} $$
   • 重置 $q$：
     (a) 执行 $Z_q$ 的测量过程，但丢弃结果。量子比特现在处于确定态 $|0\rangle$ 或 $|1\rangle$，由 $Z_q$ 列的符号指示。
     (b) 显式设置 $Z_q$ 列的符号为 $+1$，以强制状态为 $|0\rangle$。

---

备注（X 的消除）

以下两个过程是等价的；后者使用的 $X$ 更少：
$$ |a,b\rangle \xrightarrow{X \otimes X} |a \oplus 1, b \oplus 1\rangle $$
$$ |a,b\rangle \xrightarrow{\text{CNOT}} |a, a \oplus b\rangle \xrightarrow{X \otimes I} |a \oplus 1, a \oplus b\rangle \xrightarrow{\text{CNOT}} |a \oplus 1, (a \oplus 1) \oplus (a \oplus b)\rangle = |a \oplus 1, b \oplus 1\rangle $$

这产生了电路等价性：

graph LR
    subgraph Circuit Equivalence
        A[|0⟩_a] --> B[X⊗X] --> C[C]
        D[|0⟩_b] --> B
        E[|0⟩^{⊗n-2}] --> C

        F[|0⟩_a] --> G[X] --> H[C]
        I[|0⟩_b] --> J[CNOT] --> H
        K[|0⟩^{⊗n-2}] --> H
    end

---

断言（将随机测量约化为确定性测量）

以下电路具有相同的输出态分布：

graph TD
    subgraph Circuit 1
        A[|0⟩^{⊗n}] --> B[C]
        B --> C[Z]
    end

    subgraph Circuit 2
        D[|0⟩^{⊗n-1}] --> E[±X] --> F[C]
    end

    subgraph Circuit 3
        G[|+⟩] --> H[C] --> I[output +1]
        J[|0⟩^{⊗n-1}] --> H
    end

    subgraph Circuit 4
        K[|-⟩] --> L[C] --> M[output -1]
        N[|0⟩^{⊗n-1}] --> L
    end

    subgraph Circuit 5
        O[|0⟩] --> P[I] --> Q[Z] --> R[H] --> S[C]
        T[|0⟩^{⊗n-1}] --> S
    end

    subgraph Circuit 6
        U[|0⟩] --> V[X] --> W[Z] --> X[H] --> Y[C]
        Z[|0⟩^{⊗n-1}] --> Y
    end