基变换、对偶空间与张量视角下的行空间、列空间、核空间及转置核空间的关系

1. 关系图示与核心概念

1.1 对偶空间的基本关系图示

• 原空间与对偶空间：
  原空间 $U, V$和对偶空间 $U^*, V^*$通过自然配对 $\langle \cdot, \cdot \rangle$ 关联。
  自然配对是线性泛函的作用，例如 $\langle \phi, u \rangle = \phi(u)$（$\phi \in U^*$, $u \in U$）。

• 线性映射与对偶映射：
  线性映射 $L: U \to V$ 诱导对偶映射 $L^*: V^* \to U^*$，满足 $L^*(\psi) = \psi \circ L$（$\psi \in V^*$）。
  几何意义：转置 $L^*$ 将 $V^*$ 中的泛函"拉回"到 $U^*$，方向与原映射 $L$ 相反。

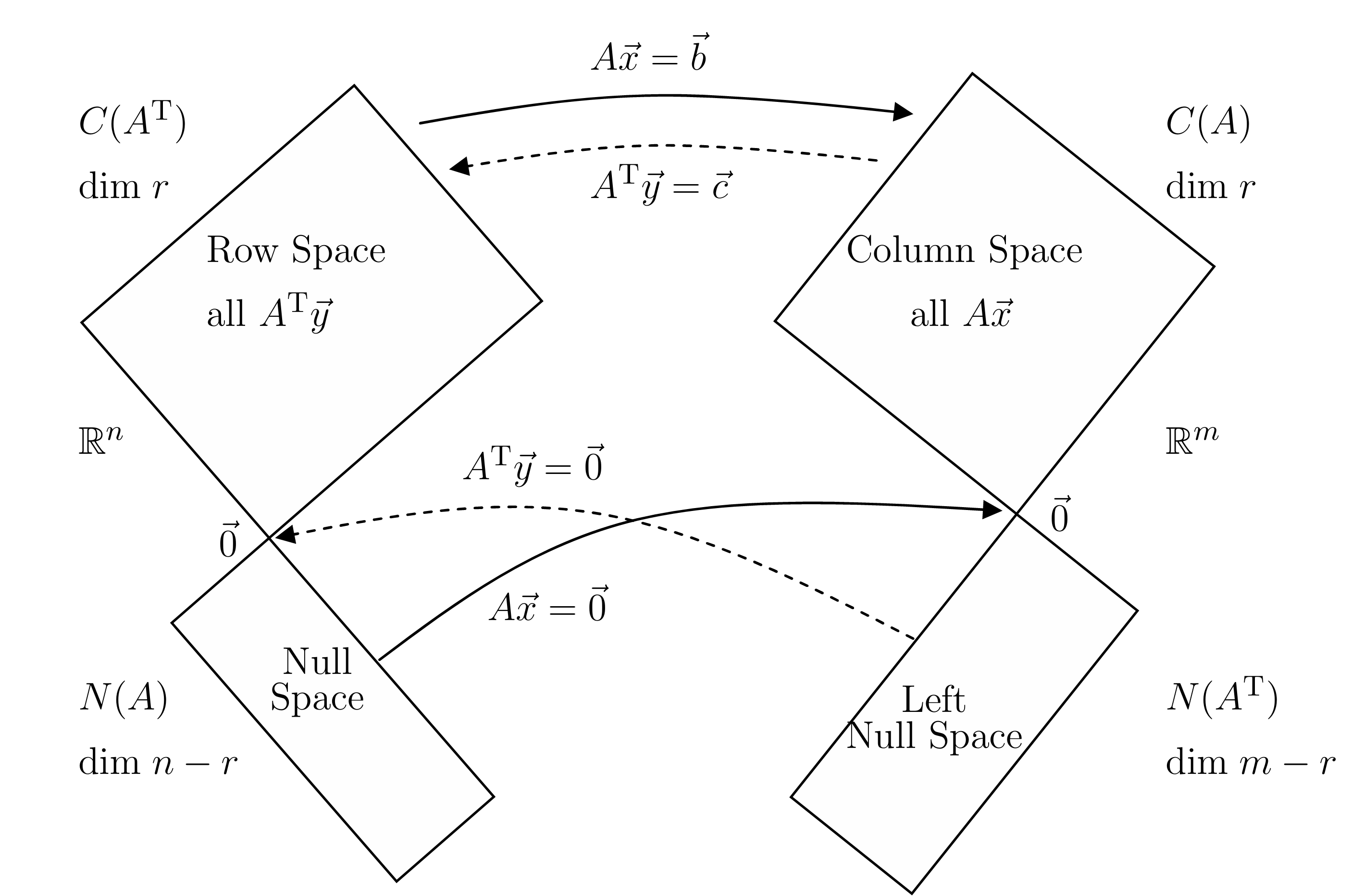
1.2 行空间、列空间、核空间与转置核空间的关系

• 行空间与列空间：
  矩阵 $A$ 的行空间 $\text{Row}(A) \subseteq U^*$，列空间 $\text{Col}(A) \subseteq V$。
  转置 $A^T$ 的列空间对应 $A$ 的行空间，行空间对应 $A$ 的列空间（见图中 $L$ 与 $L^*$ 的对应关系）。

• 核空间与左零空间：
  核空间 $\ker(A) \subseteq U$ 是行空间的正交补，左零空间 $\ker(A^T) \subseteq V^*$ 是列空间的正交补。
  图中表现为：若 $L(u) = 0$，则 $u \in \ker(L)$；若 $L^*(\psi) = 0$，则 $\psi \in \ker(L^*)$。

2. 对偶空间与对偶基的深入理解

2.1 对偶基的定义与几何意义

2.1.1 对偶基的定义：原基与对偶基的对偶关系

对偶基是线性代数中一个核心概念，它建立了一个向量空间与其对偶空间之间的深刻联系。给定一个n维线性空间V及其一组基$\{\alpha_1, \alpha_2, \ldots, \alpha_n\}$，其对偶空间$V^*$是所有从V到其基域F的线性泛函（或称线性函数）构成的空间。对偶基$\{f_1, f_2, \ldots, f_n\}$是$V^*$中的一组特殊基，它通过克罗内克δ（Kronecker delta）关系与原基$\{\alpha_i\}$相联系。具体来说，对偶基的定义要求满足以下条件：

$f_i(\alpha_j) = \delta_{ij}$

其中，$\delta_{ij}$是克罗内克δ符号，当$i=j$时其值为1，当$i \neq j$时其值为0。这个定义揭示了对偶基的本质：每个对偶基向量$f_i$都是一个线性函数，它的作用是在原基向量$\alpha_i$上取值为1，而在所有其他的原基向量$\alpha_j$（$j \neq i$）上取值为0。这种关系被称为对偶关系，它精确地刻画了原基和对偶基之间的相互作用。

2.1.2 对偶基的构造方法：从原基到对偶基的转换

构造一个给定基的对偶基，本质上是找到一组满足特定条件的线性泛函。对于一个n维线性空间V，给定一组基$\{\alpha_1, \alpha_2, \ldots, \alpha_n\}$，其对偶基$\{f_1, f_2, \ldots, f_n\}$的构造可以通过求解线性方程组来完成。每个$f_i$都是一个线性函数，可以表示为$f_i(\alpha) = c_1 x_1 + c_2 x_2 + \ldots + c_n x_n$，其中$\alpha = x_1 \alpha_1 + \ldots + x_n \alpha_n$是V中任意一个向量。根据对偶基的定义，我们需要确定每个$f_i$的系数$c_j$，使得$f_i(\alpha_j) = \delta_{ij}$。这构成了n个独立的线性方程组，每个方程组对应一个$f_i$。

更一般地，如果V中基$\{\alpha_i\}$到基$\{\beta_i\}$的过渡矩阵是A，那么$V^*$中对应的对偶基$\{f_i\}$到$\{g_i\}$的过渡矩阵B满足关系$B = (A^{-1})^T$。这个公式提供了一种系统性的方法来计算基变换时对偶基的相应变换，是连接原空间和对偶空间结构的重要桥梁。

2.1.3 对偶基的几何直观：坐标测量与线性函数

对偶基的几何直观可以理解为一种 "坐标测量"工具。在一个n维向量空间中，任意一个向量$\alpha$都可以唯一地表示为基向量的线性组合：$\alpha = x_1 \alpha_1 + x_2 \alpha_2 + \ldots + x_n \alpha_n$。这里的系数$x_i$就是向量$\alpha$在该基下的坐标。对偶基向量$f_i$的作用，就是"提取"出向量$\alpha$的第i个坐标分量。具体来说，将$f_i$作用于$\alpha$，我们得到：

$f_i(\alpha) = f_i(x_1 \alpha_1 + \ldots + x_n \alpha_n) = x_1 f_i(\alpha_1) + \ldots + x_n f_i(\alpha_n)$

根据对偶基的定义$f_i(\alpha_j) = \delta_{ij}$，上式简化为：

$f_i(\alpha) = x_i$

因此，$f_i$可以被看作是一个"投影"函数，它将任意向量$\alpha$映射到其在$\alpha_i$方向上的坐标值。这种几何解释在对偶空间与原空间之间建立了直观的联系。

2.2 内积空间中的对偶基与正交性

在内积空间中，对偶基的概念与正交性紧密相连。给定一个基$\{\mathbf{e}_i\}$，其对偶基$\{f^i\}$可以通过内积来定义。具体来说，存在一个唯一的向量$\mathbf{e}^i$（称为对偶基向量），使得对于任何向量$\mathbf{v}$，其在基$\{\mathbf{e}_i\}$下的第i个坐标$x_i$可以表示为$x_i = (\mathbf{e}^i, \mathbf{v})$。这组向量$\{\mathbf{e}^i\}$构成了所谓的互易基（reciprocal basis）。

如果原基$\{\mathbf{e}_i\}$是正交的，那么互易基向量$\mathbf{e}^i$与原基向量$\mathbf{e}_i$平行，且满足$\mathbf{e}^i = \frac{\mathbf{e}_i}{\|\mathbf{e}_i\|^2}$。如果原基是标准正交的，那么$\mathbf{e}^i = \mathbf{e}_i$，即原基和互易基完全相同。在这种情况下，测量一个向量的坐标（即应用对偶基泛函）就等同于计算该向量与基向量的内积。这种简洁的关系是内积空间中正交基强大功能的体现。

2.3 对偶空间与原空间的同构关系

在有限维向量空间中，一个空间V和它的对偶空间V是同构的，这意味着它们在结构上是完全相同的。更重要的是，V和它的双重对偶空间V之间存在一个自然的同构关系*，这个同构不依赖于基的选择。这个自然同构允许我们将V和V*等同起来，从而可以说V是V的对偶空间。这种互为对偶的关系是理解对偶性几何直观的核心。

当我们考虑一个内积空间时，内积结构提供了一个从V到V*的特定同构，称为黎兹表示定理（Riesz representation theorem）。这个同构将每个向量$\mathbf{v} \in V$映射到一个线性泛函$f_{\mathbf{v}} \in V^*$，定义为$f_{\mathbf{v}}(\mathbf{w}) = (\mathbf{v}, \mathbf{w})$。这个同构是共轭线性的（在实数域上是线性的），并且它依赖于内积的选择。

3. 基变换与空间关系

3.1 行空间、列空间与核空间的关系

从对偶空间的视角来看，矩阵的行空间、列空间、核空间和左零空间之间存在着深刻的对称关系。对于一个$m \times n$矩阵$A$，其行空间是$A$的所有行向量张成的空间，属于$\mathbb{R}^n$；列空间是$A$的所有列向量张成的空间，属于$\mathbb{R}^m$。

根据秩-零化度定理，有：

• $\dim(\text{Row}(A)) = \dim(\text{Col}(A)) = \text{rank}(A)$
• $\dim(\ker(A)) = n - \text{rank}(A)$
• $\dim(\ker(A^T)) = m - \text{rank}(A)$

这些空间之间存在正交补关系：

• $\ker(A)$是$\text{Row}(A)$在$\mathbb{R}^n$中的正交补
• $\ker(A^T)$是$\text{Col}(A)$在$\mathbb{R}^m$中的正交补

3.2 基变换下的空间行为

当进行基变换时，矩阵的行空间、列空间、核空间和左零空间的行为可以通过对偶性来理解。设$P$和$Q$分别是$\mathbb{R}^n$和$\mathbb{R}^m$中的可逆矩阵（基变换矩阵），则矩阵$A$在新基下的表示为$A' = Q^{-1} A P$。

在这种基变换下：

• 行空间的变化：$\text{Row}(A') = P^{-1} \text{Row}(A)$
• 列空间的变化：$\text{Col}(A') = Q^{-1} \text{Col}(A)$
• 核空间的变化：$\ker(A') = P^{-1} \ker(A)$
• 左零空间的变化：$\ker((A')^T) = Q^{-1} \ker(A^T)$

这些变换规律表明，虽然这些空间在基变换下会改变其具体的表示形式，但它们之间的维度关系和正交补关系保持不变。

4. 张量视角下的空间关系

4.1 张量积与多线性代数

从张量的视角来看，矩阵可以视为一个(1,1)型张量，即一个线性映射$V \to W$，或者等价地，一个双线性形式$V^* \times W \to \mathbb{R}$。这种观点将行空间、列空间、核空间和左零空间统一在一个框架下。

具体来说，矩阵$A$可以表示为：
$$A = \sum_{i,j} a_{ij} \mathbf{e}_i \otimes \mathbf{f}^j$$
其中$\{\mathbf{e}_i\}$是$V$的基，$\{\mathbf{f}^j\}$是$W^*$的对偶基。

4.2 张量视角下的空间关系

在张量语言中：

• 行空间对应于$A$作为线性映射$W^* \to V$的像空间
• 列空间对应于$A$作为线性映射$V \to W$的像空间
• 核空间对应于$A$作为线性映射$V \to W$的零空间
• 左零空间对应于$A$作为线性映射$W^* \to V$的零空间