Ch 2.4 Hahn-Banach 定理与凸集
Hahn-Banach 定理(延拓)
子空间上的有界线性泛函延拓到全空间
定义(拟范数)
若 $X$ 是实向量空间,$P: X \to \mathbb{R}$ 称为一个拟范数,如果:
- $\forall x, y \in X,\quad p(x+y) \leq p(x) + p(y)$ (三角不等式)
- $\forall \lambda \geq 0,\quad p(\lambda x) = \lambda p(x)$ (正齐性)
若 $p$ 是一个拟范数且满足 $p(\lambda x) = |\lambda| p(x),\ \forall \lambda \in \mathbb{R}$(称为绝对齐次性),称 $p$ 是一个半范数。
注
-
由 1 和 $p(0) \leq 2p(0) \Rightarrow p(0) \geq 0$
-
若 2 成立,则
$$ p(\pm x) = p(x) \Rightarrow 2p(x) = p(x) + p(-x) \geq p(0) \geq 0. $$
即:若 $p$ 是半范数时,$p$ 是非负的。 -
范数与半范数的区别在于是否区分零点,即:
$$ p(x) = 0 \Leftrightarrow x = 0 $$
例子: $\forall f \in C[0,1],\quad p(f) \stackrel{\text{定义}}{=} |f(x_0)|$,其中 $x_0 \in [0,1]$. 则 $p$ 是 $C[0,1]$ 上的半范数。
定理(实 Hahn-Banach)
设 $X$ 是实线性空间,$p: X \to \mathbb{R}$ 是一个拟范数,$Y \subseteq X$ 是 $X$ 的子空间。$\phi: Y \to \mathbb{R}$ 是线性映射,满足 $\phi(x) \leq p(x),\ \forall x \in Y$。则存在线性映射 $\Phi: X \to \mathbb{R}$,满足:
- $\Phi|_Y = \phi$
- $\forall x \in X,\quad \Phi(x) \leq p(x)$
注: 将线性子空间上的线性映射延拓至全空间是容易的。这里的难点在于延拓的同时保持原先“线性映射”的约束(即 $\forall x \in Y,\ \Phi(x) \leq p(x)$)。
引理 1
假设 $X, Y, p, \phi$ 满足定理条件。记 $x_0 \in X \setminus Y$,$\widetilde{Y} \stackrel{\text{定义}}{=} Y \oplus \operatorname{span}\{x_0\}$。则存在线性映射 $\widehat{\phi}: \widetilde{Y} \to \mathbb{R}$,满足:
- $\widehat{\phi}|_Y = \phi$
- $\forall x \in \widetilde{Y},\quad \widehat{\phi}(x) \leq p(x)$
证明
由要求,任取 $x \in \widetilde{Y}$,$\exists\, y \in Y$ 且 $\lambda \in \mathbb{R}$,s.t. $x = y + \lambda x_0$
定义 $\widehat{\phi}(x) = \phi(y) + t\lambda$ (若 $\widehat{\phi}$ 是线性、满足 ①②,则 $\widehat{\phi}(x) = \phi(y) + \lambda \widehat{\phi}(x_0)$)
不难验证:$\widehat{\phi}|_Y = \phi$. 为了满足2:
$$ \widehat{\phi}(x) \leq p(x) \iff \phi(y) + \lambda a \leq p(y + \lambda x_0) \quad \forall y \in Y,\ \forall \lambda \in \mathbb{R}. $$
不妨假设 $\lambda \neq 0$,
④ $\iff |\lambda| \left( \phi(|\lambda|^{-1} y) + \operatorname{sgn}\lambda \cdot a \right) \leq |\lambda| \, p(|\lambda|^{-1} y + (\operatorname{sgn}\lambda) x_0)$
$\iff \phi(y) \pm a \leq p(y \pm x_0),\quad \forall y \in Y$
$\iff \phi(y) - p(y - x_0) \leq a \leq p(y + x_0) - \phi(y),\quad \forall y \in Y$
任取 $y, \tilde{y} \in Y$:
$$ \phi(y) + \phi(\tilde{y}) = \phi(y + \tilde{y}) \leq p(y + \tilde{y}) \leq p(y + x_0) + p(\tilde{y} - x_0) $$
$$\Rightarrow\quad \phi(\tilde{y}) - p(\tilde{y} - x_0) \leq p(y + x_0) - \phi(y)$$
$$\Rightarrow\quad \sup_{\tilde{y} \in Y} \left( \phi(\tilde{y}) - p(\tilde{y} - x_0) \right) \leq \inf_{y \in Y} \left( p(y + x_0) - \phi(y) \right)$$
$\Rightarrow$ $a$ 存在
定理证明
利用 Zorn 引理 $\Rightarrow$ H–B 定理。记
$$\mathcal{P} = \left\{ (Z, \chi) \ \middle| \ \begin{array}{l} Z \subseteq X \text{(线性子空间)}, \\ \chi: Z \to \mathbb{R} \text{(线性映射),满足} \\ ①\ Y \subseteq Z \\ ②\ \chi|_Y = \phi \\ ③\ \chi(x) \leq p(x),\ \forall x \in Z \end{array} \right\}$$
$\mathcal{P}$ 上定义偏序关系,即:
$$(Z, \chi) \preccurlyeq (\widehat{Z}, \widehat{\chi}) \quad \text{如果} \quad Z \subseteq \widehat{Z} \quad \text{且} \quad \widehat{\chi}\big|_Z = \chi.$$
可以验证:
- 若 $S \subseteq \mathcal{P}$ 是全序子集,则令 $Z_0 \stackrel{\text{定义}}{=} \bigcup_{(Z,\chi)\in S} Z$。$\forall x \in Z_0.\ (\Rightarrow \exists (Z,\chi) \in S,\ \text{s.t.}\ x \in Z)\quad \chi_0(x) \stackrel{\text{定义}}{=} \chi(x)$. 由此,$(Z_0, \chi_0)$ 是 $S$ 的上界。
- 由 Zorn 引理,$\exists \mathcal{P}$ 的一个极大元 $(\widehat{Z}, \widehat{\chi})$ 满足 $\widehat{Z} = X$ (否则由引理1,可以构造 $(Z', \chi') \in \mathcal{P}$,s.t. $\widehat{Z} \subsetneq Z'$ 且 $\chi'\big|_{\widehat{Z}} = \widehat{\chi}$,这与极大元性质矛盾
推论1
若 $X$ 是 $\mathbb{R}$ 上的赋范空间,$Y \subseteq X$ 是子空间,$\phi: Y \to \mathbb{R}$ 是线性映射且 $\phi \in Y^*$,
则 $\exists\, \Phi \in X^*$,s.t. $\Phi|_Y = \phi$ 且 $\|\Phi\| = \|\phi\|$。
证明:
取 $p(x) \stackrel{\text{定义}}{=} \|\phi\| \|x\|$,由 H-B 定理,$\exists\, \Phi: X \to \mathbb{R}$,s.t.
- $\Phi|_Y = \phi$。
- $\Phi(x) \leq \|\phi\| \|x\|,\quad \forall x \in X \implies |\Phi(x)| = \Phi(\operatorname{sgn}\Phi(x)\cdot x) \leq \|\phi\| \|x\|\implies \|\Phi\| = \|\phi\|$。
推论2(复 Hahn-Banach)
复线性泛函和实线性泛函
复线性泛函的实部和虚部都是实线性泛函。
考虑 $f(x) = \varphi(x) + i \phi(x)$,则有 $\varphi(x) = \frac{f(x) + \overline{f(x)}}{2},\quad \phi(x) = \frac{f(x) - \overline{f(x)}}{2i}$
于是 $\varphi(\alpha x + \beta y) = \frac{f(\alpha x + \beta y) + \overline{f(\alpha x + \beta y)}}{2} = \frac{\alpha f(x) + \beta f(y) + \overline{\alpha f(x) + \beta f(y)}}{2} = \alpha \varphi(x) + \beta \varphi(y)$,同理可证 $\phi$ 也是实线性泛函。
另外,我们有 $f(ix) = if(x)$,即 $\varphi(ix) + i \phi(ix) = i \varphi(x) - \phi(x)$,从而 $\varphi(ix) = -\phi(x),\quad \phi(ix) = \varphi(x)$。
故 $f(x) = \varphi(x) - i \varphi(ix)$, 即复线性泛函由其实部唯一确定。
若 $X$ 是 $\mathbb{C}$ 上的赋范空间,$Y \subseteq X$ 是线性子空间,$\gamma \in L(Y; \mathbb{C})$,则 $\exists\, \Psi \in L(X; \mathbb{C})$,s.t.
- $\Psi|_Y = \gamma$,
- $\|\Psi\| = \|\gamma\|$。
证明
记 $\phi(x) \stackrel{\text{定义}}{=} \operatorname{Re} \gamma(x)$,则 $|\phi(x)| \leq \|\gamma\| \|x\|$。
$Y = (Y, +, \cdot, \mathbb{C}) \implies Y = (Y, +, \cdot, \mathbb{R})$。由推论1,$\exists\, \Phi \in L((X, +, \cdot, \mathbb{R}); \mathbb{R})$,s.t. $\forall x \in X,\quad |\Phi(x)| \leq \|\gamma\| \|x\|$。
由 $\phi(x) = \operatorname{Re} \gamma(x) \implies \Phi(ix) = \operatorname{Re} (\gamma(ix)) = -\operatorname{Im} \gamma(x)\implies \gamma(x) = \operatorname{Re} \gamma(x) + i \operatorname{Im} \gamma(x) = \Phi(x) - i \Phi(ix)$
记 $\Psi(x) \stackrel{\text{定义}}{=} \Phi(x) - i \Phi(ix)$,则
- $\forall x, y \in X,\ a+ib \in \mathbb{C}$ $\Psi((a+ib)x + y) = \Phi(ax + ibx + y) - i \Phi(i(ax+y) - bx)$
$= a\Phi(x) + b\Phi(ix) + \Phi(y) - i \left[ -b\Phi(x) + a\Phi(ix) + \Phi(iy) \right]$
$= (a+ib)\Psi(x) + \Psi(y) \implies \Psi$ 是复线性的。 - $\Psi|_Y = \gamma$
- $\Psi(x) = |\Psi(x)| e^{i\theta_x} \implies |\Psi(x)| = \Psi(e^{-i\theta_x} x) = \Phi(e^{-i\theta_x} x) \leq \|\gamma\| \|x\|\implies \|\Psi\| = \|\gamma\|$。
几个应用
命题3
若 $X$ 是赋范空间,$\forall x \in X \setminus \{0\}$,$\exists f \in X^*$,s.t. $f(x) = \|x\|$ 且 $\|f\| = 1$。
证明
记 $Y = \operatorname{span}\{x\}$。$\phi(ax) \stackrel{\text{定义}}{=} a\|x\|$。$\Rightarrow |\phi(y)| = |\phi(ax)| = |a|\|x\| = \|ax\| = \|y\|$ $\Rightarrow \|\phi\| = 1$。$\implies$(由 H-B 定理)$\exists f \in X^*$,s.t. $f|_Y = \phi$(即 $f(x) = \|x\|$)且 $\|f\| = 1$。
由命题3推出如下结论:即 $X^*$($X$ 上的坐标轴)可以区分 $X$ 中的任意两点。
推论4
- 若 $x, y \in X$ 且 $x \neq y$,则 $\exists f \in X^*$,s.t. $f(x) \neq f(y)$;
- 若 $x \in X$,满足 $\forall f \in X^*$ 有 $f(x) = 0$,则 $x = 0$。
证明
只需证明1。由命题3,$\exists f \in X^*$,s.t. $f(x-y) = \|x-y\| \neq 0 \implies f(x) \neq f(y)$。
命题5
若 $X$ 是赋范空间,$M \subseteq X$ 是线性子空间,$x_0 \in X$ 且 $\operatorname{dist}(x_0, M) = d > 0$。则 $\exists f \in X^*$ 满足
- $f|_M \equiv 0$
- $f(x_0) = d$
- $\|f\| = 1$。

证明
-
对于 Hilbert 空间上。假设 $\{e_\alpha\}_{\alpha \in \Lambda}$ 是 $M$ 的规范正交基。则 $(x_0)_M \stackrel{\text{定义}}{=} \sum_{\alpha \in \Lambda} \langle x_0, e_\alpha \rangle e_\alpha$ 且 $x_0 - (x_0)_M \perp M$ $\implies d = \|x_0 - (x_0)_M\|$。$\implies f(x) = \langle x, \frac{x_0 - (x_0)_M}{\|x_0 - (x_0)_M\|} \rangle \implies f$ 满足 ①②③。
-
对于一般的 Banach 空间。记 $Y = M \oplus \operatorname{span}\{x_0\}$。$\forall y \in Y$,$\exists !\ x \in M,\ t \in \mathbb{F}$,s.t. $y = x + tx_0$。则 $f(y) \stackrel{\text{定义}}{=} td \implies$ ①②成立。对 $\forall f \in Y^*$,$\forall y \in M$,$|f(y)| = |t|d = |t| \operatorname{dist}(x_0, M) \leq |t| \|x_0 + \frac{x}{t}\| = \|y\|$(取 $y = x + tx_0$, $t \neq 0$)。$\implies f \in Y^*$ 且 $\|f\| \leq 1$。另证:$d = |f(x_0)| \stackrel{\text{取}}{=} \sup_{h \in M} |f(x_0 - h)| \leq \|f\| \|x_0 - h\| \implies d \leq \|f\| d \implies \|f\| \geq 1 \implies \|f\| = 1$。由 H-B 定理,$\exists f \in X^*$ 满足 ①②③。
推论6
- 假设 $M \subseteq X$,则 $x \in \overline{\operatorname{span}\, M} \iff \forall f \in X^*$ 满足 $f|_M = 0$,有 $f(x) = 0$。
- 若 $X$ 是实赋范空间,$S \subseteq X$。称 $S^\perp$ 是 $S$ 的零化子空间,如果 $S^\perp = \{ f \in X^* \mid f|_S = 0 \}$。
注: $x \in \overline{M}$($M$ 是 $X$ 的线性子空间)$\iff \forall f \in M^\perp$, $f(x) = 0$($\Rightarrow M$ 是 $X$ 的稠密子集 $\iff M^\perp = \{0\}$)
Hahn-Banach 定理(凸集分离)
包括凸集与点的分离、凸集与凸集的分离和凸闭集与凸紧集的分离
引入
由$\mathbb{R}^n$的凸投影定理(有限性):
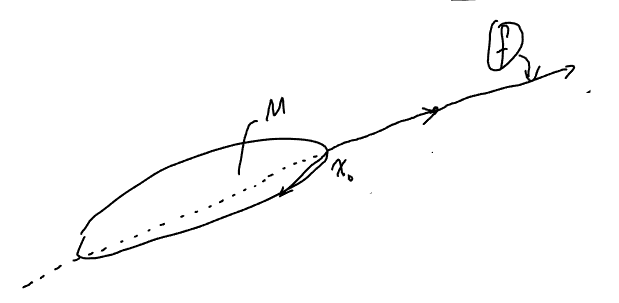
若 $M$ 为凸闭集,$x \notin M$。
$\Rightarrow$ ① $\exists x_0 \in M$,s.t. $\|x - x_0\| = \text{dist}(x, M)$
② $\forall y \in M$, $(x - x_0, y - x_0) \leq 0$
$\forall z \in \mathbb{R}^n$, 记 $f(z) = (z, x - x_0)$
则 $\forall y \in M$,
$f(x) - f(y) = (x - y, x - x_0) = (x - x_0, x - x_0) - (y - x_0, x - x_0)$
$= \|x - x_0\|^2 - (y - x_0, x - x_0) \geq 0$
一些定义和引理
定义(超平面,仿射超平面)
- 设 $X$ 是实赋范空间,如果 $M$ 是闭子空间且 $\text{codim}(M) = \text{dist}(X/M) = 1$,称 $M$ 是 $X$ 的超平面。
- 如果 $\tilde{M}$ 是超平面 $M$ 的平移,称 $\tilde{M}$ 是仿射超平面。
定义(开半空间)
若 $f \in X^*$ 且 $f \neq 0$, $c \in \mathbb{R}$,称 $\{x \in X \mid f(x) > c\}$ 为开半空间。
命题7
$M \subseteq X$ 是仿射超平面 $\Leftrightarrow \exists 0 \neq f \in X^*$ 以及 $c \in \mathbb{R}$,s.t. $M = f^{-1}(c) = \{x \in X \mid f(x) = c\}$。
证明
“$\Rightarrow$”
由定义,$\exists Y \subseteq X$ 超平面以及 $x_0 \in Y$,s.t. $M = Y + x_0$。$\Rightarrow Y = Y \oplus \text{span}\{x_0\}$。(由补子空间性质)
由命题5的结论,$\exists f \in X^*$,s.t. $f(y + t x_0) = t \cdot \text{dist}(x_0, M) \Rightarrow f^{-1}(0) = Y \quad \Rightarrow \quad M = f^{-1}(f(x_0))$
“$\Leftarrow$”
设 $Y = f^{-1}(0)$,$f(x_0) = c$,则 $M = Y + x_0$。由于 $f \in X^* \Rightarrow Y = \ker f$ 是闭子空间。
$\forall x \in X$,$x = \frac{f(x)}{f(y_0)} y_0 + x - \frac{f(x)}{f(y_0)} y_0 $,于是 $X = \ker f \oplus \text{span}\{y_0\}$,其中 $f(y_0) = 1$,且 $(\ker f) \cap \text{span}\{y_0\} = \{0\}$。
引理8
若 $X$ 是实赋范空间,$A \subseteq X$ 是凸集。则
- $\text{int}(A)$ 以及 $\overline{A}$ 是凸集。
- 如果 $\text{int}(A) \neq \emptyset$,则 $A \subseteq \overline{\text{int} A}$。
证明:
- 由定义直接验证;
- 假设 $x_0 \in \text{int}(A) \Rightarrow \exists \delta > 0$,s.t. $B(x_0; \delta) \subseteq \text{int}(A) \subseteq A$。
任取 $x \in A$,记 $U_x = \left\{ tx + (1-t)y \mid y \in B(x_0; \delta), t \in ]0,1] \right\}$。$\Rightarrow U_x \subseteq \text{int}(A)$
$\Rightarrow x \in \overline{U_x} \subseteq \overline{\text{int}(A)}$
(图示:点 $x$、点 $x_0$、区域 $U_x$ 及其包含关系示意)
引理9
若 $X$ 是实赋范空间,$A \subseteq X$ 是凸集且 $\text{int}(A) \neq \emptyset$。若存在非零 $f \in X^*$ 以及 $c \in \mathbb{R}$,s.t. $\forall x \in \text{int}(A)$,$f(x) \geq c$。则 $\forall x \in A$,$f(x) \geq c$,且 $\forall x \in \text{int}(A)$,$f(x) > c$。 (即严格区分内点与边界)
证明
由引理8,$\overline{\text{int}(A)} \supseteq A \Rightarrow \forall x \in A$,$f(x) \geq c$。假设 $x_0 \in \text{int}(A)$,$x_0 \in X$ 满足 $f(x_0) = 1 \Rightarrow \exists t > 0$,s.t. $x \pm t x_0 \in A \Rightarrow f(x) = f(x - t x_0) + f(t x_0) \geq c + t f(x_0) > c$
Minkowski 泛函
在线性空间上引入“距离”
定义
若 $K$ 是 $(X, +, \cdot, \mathbb{F})$($\mathbb{F} = \mathbb{R}$ 或 $\mathbb{C}$)中的凸集,则由 $K$ 诱导的 Minkowski 泛函 $P_K: X \to [0, +\infty]$ 定义为:
$$ P_K(x) \overset{\text{def}}{=} \inf \left\{ r \in \mathbb{R} \mid r > 0,\ x \in rK \right\}, \quad \forall x \in X. $$
其中,约定 $\inf \emptyset = +\infty$。
$P_K(x)$ 的几何意义:即零点沿着 $x$ 方向“经伸缩变换”至集合边界时的相似系数。
几个例子
1
取 $U = \{ \|x\| \leq 1 \}$,则 $P_U(x) = \|x\|$。
(若 $\hat{U} = \{ \|x\| < 1 \}$,则 $P_{\hat{U}}(x) = \|x\|$)
2
设 $X = (X, +, \cdot, \mathbb{R})$,$f$ 是 $X$ 上的线性泛函,$a > 0$。令 $K \overset{\text{def}}{=} \{ x \in X \mid |f(x)| \leq a \}$,则:
$$ P_K(x) = \frac{1}{a} |f(x)| \quad \text{且} \quad P_K \text{是半范数}. $$
定义: 吸收集
为了保证 $P_K$ 点点有限,引入“吸收集”,即:
若 $X = (X, +, \cdot, \mathbb{F})$,$K \subseteq X$,称 $K$ 在 $X$ 中是吸收的,如果 $\forall x \in X$,$\exists \lambda > 0$,s.t.:
$$ x \in rK \quad \forall r \in \mathbb{F} \text{ 且 } |r| \geq \lambda \quad \Rightarrow \quad 0 \in K \text{ 且 } P_K(0) = 0. $$
定义: 代数内点
若 $X = (X, +, \cdot, \mathbb{R})$,$x_0 \in A$ 称为 $A$ 的代数内点,如果 $\forall x \in X$,$\exists t_x > 0$,使得:
$$ x_0 + [0, t_x]x \subseteq A, $$
或等价地:
$$ \left\{ x_0 + rx \mid r \in [0, t_x] \right\} \subseteq A. $$
几何意义:从点 $x_0$ 出发,沿任意方向 $x$,都可以在 $A$ 内走一小段距离。
命题4
$X = (X, +, \cdot, \mathbb{R})$,则 $K$ 是吸收集 $\Leftrightarrow$ $0$ 是 $K$ 的代数内点。
由定义可知,若 $K$ 是吸收集,则 $\forall x \in X$,有 $P_K(x) < +\infty$。
可以证明:若 $K$ 是凸集,则 $\forall x \in X$,$P_K(x) < +\infty \Leftrightarrow K$ 是吸收集。
定义: 平衡集
为了进一步保证 $P_K(x)$ 是半范数,引入“平衡”的概念,即:
若 $X = (X, +, \cdot, \mathbb{R})$,$K \subseteq X$,称 $K$ 是 $X$ 中的平衡集,如果 $\forall |a| \leq 1$,$\forall s \in K$,有 $as \in K$。
即:$\forall |a| \leq 1$,$aK \subseteq K$。
若 $K$ 是凸集,则 $K$ 是平衡集 $\Leftrightarrow \forall |a| = 1$,$aK \subseteq K$。
定理: 集合分类
定理:若 $K$ 是 $X = (X, +, \cdot, \mathbb{R})$ 中的集合,则:
-
若 $K$ 是凸吸收集,则 $P_K$ 满足次可加性(或称次可加性),且 $P_K$ 是拟范数。
-
若 $K$ 是平衡吸收集,则 $P_K$ 满足绝对齐次性。(即:$P_K(\lambda x) = |\lambda| P_K(x)$,$\forall \lambda \in \mathbb{R}$)。
-
若 $K$ 是平衡凸吸收集,则 $P_K$ 是半范数, 且:$P_K(x) = \frac{1}{\sup\{ r > 0 \mid rx \in K \}}$
吸收:保证 $P_K(x) < +\infty \Rightarrow$ 保证次可加性有效。
凸:保证三角不等式(见图3)。
平衡:保证绝对齐次性。
证明
- $K$ 是凸吸收集,下证“次可加性”以及“正齐次性”。
-
次可加性,即:$P_K(x+y) \leq P_K(x) + P_K(y)$。
由 $P_K(x)$ 的定义,$\forall \varepsilon > 0$,$\exists r_x > 0$,s.t. $r_x < P_K(x) + \varepsilon$ 且 $\frac{x}{r_x} \in K$;同理 $\frac{y}{r_y} \in K$。
$\Rightarrow \frac{r_x}{r_x + r_y} \cdot \frac{x}{r_x} + \frac{r_y}{r_x + r_y} \cdot \frac{y}{r_y} \in K$
即:$\frac{x+y}{r_x + r_y} \in K \Rightarrow P_K(x+y) \leq r_x + r_y \leq P_K(x) + P_K(y) + 2\varepsilon \Rightarrow$ 结论成立。
-
正齐次性,即:$P_K(\lambda x) = \lambda P_K(x)$,$\forall \lambda > 0$。
由 $P_K(x)$ 的定义,$\forall \varepsilon > 0$,$\exists r_x > 0$,s.t. $r_x < P_K(x) + \varepsilon$ 且 $\frac{x}{r_x} \in K$。
$\Rightarrow \frac{\lambda x}{\lambda r_x} \in K \Rightarrow P_K(\lambda x) \leq \lambda r_x \leq \lambda (P_K(x) + \varepsilon) \Rightarrow P_K(\lambda x) \leq \lambda P_K(x)$。
又 $\frac{1}{\lambda} \cdot (\lambda x) = x \in K \Rightarrow P_K(x) \leq \frac{1}{\lambda} P_K(\lambda x) \Rightarrow P_K(\lambda x) \geq \lambda P_K(x)$。
故 $P_K(\lambda x) = \lambda P_K(x)$,$\Rightarrow P_K$ 是拟范数。
-
$K$ 是平衡吸收集,则 $P_K(\lambda x) = |\lambda| P_K(x)$。由上一问,当 $\lambda > 0$ 时,$P_K(\lambda x) = \lambda P_K(x)$。
只需证明:$P_K(-x) = P_K(x)$。
由 $P_K(x)$ 的定义,$\forall \varepsilon > 0$,$\exists r_x > 0$,s.t. $r_x < P_K(x) + \varepsilon$ 且 $\frac{x}{r_x} \in K$。
$\Rightarrow \frac{-x}{r_x} \in K$ (因 $K$ 平衡)$\Rightarrow P_K(-x) \leq r_x \leq P_K(x) + \varepsilon \Rightarrow P_K(-x) \leq P_K(x)$。
又 $P_K(x) = P_K(-(-x)) \leq P_K(-x)$,故 $P_K(x) = P_K(-x)$。
因此,$P_K(\lambda x) = |\lambda| P_K(x)$,即满足绝对齐次性。
定理 (Hahn-Banach 几何形式)
设 $X$ 是实赋范空间,$A, B \subseteq X$ 是非空凸集。
- 若 $0 \in A$ 且 $x_0 \notin \bar{A}$。则存在非零 $f \in X^*$ 以及 $c \in \mathbb{R}$,使得:
$$ f(x_0) \leq c \leq f(a), \quad \forall a \in A.\\ c < f(\tilde{a}), \quad \forall \tilde{a} \in \mathrm{int}(A). $$ - 若 $A \cap B \neq \phi$ 且 $\mathrm{int}(A) \neq \phi, \, B \neq \phi$,则存在非零 $f \in X^*$ 以及 $c \in \mathbb{R}$,使得:
$$ \sup_{a \in A} f(a) \leq c \leq \inf_{b \in B} f(b).\\ f(\tilde{a}) < c, \quad \forall \tilde{a} \in \mathrm{int}(A).\\ $$ - 若 $A$ 是闭集,$B$ 是紧集且 $A \cap B = \phi$,则存在连续的线性泛函 $f \in X^*$ 使得:
$$ \sup_{a \in A} f(a) < \inf_{b \in B} f(B). $$
证明
1
由于 $x_0 \notin \bar{A}$ 且 $\bar{A}$ 是闭凸集,考虑集合 $C = \bar{A} - x_0$。则:
$C$ 是闭凸集
$0 \notin C$(否则 $x_0 \in \bar{A}$,矛盾)
由 $0 \notin C$且$C$闭,存在$\delta > 0$使得$B(0, \delta) \cap C = \phi$。
定义集合 $K = B(0, \delta) + \bar{A}$,则:
$K$ 是凸开集(作为开球与凸集的Minkowski和)
$0 \in K$(因 \$0 \in \bar{A}$)
$x_0 \notin K$(否则存在 $a \in \bar{A}$ 使得 $x_0 - a \in B(0, \delta)$,即 $x_0 - a \in C \cap B(0, \delta)$,矛盾)
考虑 $K$ 的 Minkowski 泛函 $p_K$。由于 $K$ 是凸吸收开集,$p_K$ 是连续次线性泛函。
在子空间 $M = \text{span}\{x_0\}$ 上定义线性泛函:
$f_0(λx_0) = λp_K(x_0)$
验证 $f_0 \leq p_K$ 在 $M$ 上:
当 $λ \geq 0$:$f_0(λx_0) = λp_K(x_0) = p_K(λx_0)$
当 $λ < 0$:$f_0(λx_0) = λp_K(x_0) < 0 \leq p_K(λx_0)$
由 Hahn-Banach 定理(解析形式),存在 $X$ 上的线性泛函 $f$ 延拓 $f_0$ 且满足 $f \leq p_K$。
由于 $p_K$ 连续,$f$ 也连续,即 $f \in X^*$。
取 $c = p_K(x_0)$,则:
$f(x_0) = p_K(x_0) = c$
对任意 $a \in A$,有 $a \in K$,故 $p_K(a) \leq 1$,但需更精确估计:
实际上,对任意 $a \in \bar{A}$,由 $K$ 的定义,$a + B(0, \delta) \subset K$,故 $p_K(a) \leq 1$。更精细地:
对任意 $\epsilon > 0$,有 $a \in (1+\epsilon)K$,故 $p_K(a) \leq 1$。
因此 $f(a) \leq p_K(a) \leq 1$,而 $f(x_0) = p_K(x_0)$。
由于 $x_0 \notin K$,有 $p_K(x_0) \geq 1$,故:
$f(x_0) = p_K(x_0) \geq 1 \geq p_K(a) \geq f(a) \quad \forall a \in A$
对 $\tilde{a} \in \text{int}(A)$,存在 $r > 0$ 使得 $\tilde{a} + B(0, r) \subset A$,故 $p_K(\tilde{a}) < 1$,从而:
$f(\tilde{a}) \leq p_K(\tilde{a}) < 1 \leq p_K(x_0) = c$
2
由条件知 $\text{int}(A) \cap B = \phi$(否则与结论矛盾)。
考虑集合 $C = \text{int}(A) - B = \{a - b : a \in \text{int}(A), b \in B\}$,则:
$C$ 是凸集(作为两个凸集的Minkowski差)
$0 ∉ C$(因 $\text{int}(A) \cap B = \phi$)
$C$ 是开集(因 $\text{int}(A)$ 开)
由第一部分证明方法,存在非零 $f \in X^*$ 使得:
$f(c) > 0 \quad \forall c \in C$
即对任意 $a \in \text{int}(A)$,$b \in B$,有:
$f(a - b) > 0 \quad \Rightarrow \quad f(a) > f(b)$
令 $c = \inf_{b \in B} f(b)$,则:
$f(a) \geq c$ 对 $a \in A$(由连续性及 $A \subset \overline{\text{int}(A)}$)
$f(\tilde{a}) > c$ 对 $\tilde{a} \in \text{int}(A)$
$c \leq f(b)$ 对 $b \in B$
因此:
$\sup_{a \in A} f(a) \leq c \leq \inf_{b \in B} f(b), \quad f(\tilde{a}) < c \quad \forall \tilde{a} \in \text{int}(A)$
3
由于 $A$ 闭、$B$ 紧且不相交,存在 $\delta > 0$ 使得:
$d(A, B) = \inf\{\|a-b\| : a \in A, b \in B\} > 0$
令 $U = A + B(0, \delta/2)$,则$U$ 是凸开集,$U \cap B = \phi$且$A \subset U$
由第二部分(取 $A = U$,$B = B$),存在非零 $f \in X^*$ 使得:
$\sup_{u \in U} f(u) \leq \inf_{b \in B} f(b)$
由于 $A \subset U$,有:
$\sup_{a \in A} f(a) \leq \sup_{u \in U} f(u) \leq \inf_{b \in B} f(b)$
但需证明严格不等式。假设相等,则存在序列 $\{a_n\} \subset A$,$\{b_n\} \subset B$ 使得:
$\lim f(a_n) = \lim f(b_n) = c$
由 $B$ 紧,存在子列 $b_{n_k} \to b \in B$,且 $f(b) = c$。
对任意 $\epsilon > 0$,存在 $a \in A$ 使得 $f(a) > c - \epsilon$。考虑点 $a + \delta v$,其中 $v$ 满足 $f(v) > 0$,则:
$f(a + \delta v) = f(a) + \delta f(v) > c - \epsilon + \delta f(v)$
取 $\epsilon$ 充分小,可得 $f(a + \delta v) > c$,但 $a + \delta v \in U$,与 $\sup_{u \in U} f(u) \leq c$ 矛盾。